IB數學考點解析—你了解正態分布嗎？

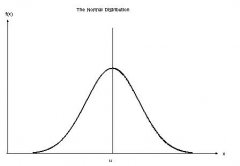
　　IB數學統計部分大家族中有許許多多個分布，其中Normal Distribution（正態分布）是舉足輕重的一員。它是一個呈鐘型的（bell shape）對稱（symmetrical）分布曲線。別小瞧這樣一個外表并不十分出眾的曲線，它在各種數學分布中可謂地位崇高，在各個實用領域也頗受重用。今天A加未來小編就帶大家一起來解析一下IB數學考點中有關正態分布的相關內容，希望能夠幫助大家更好的理解這部分內容。
 

 

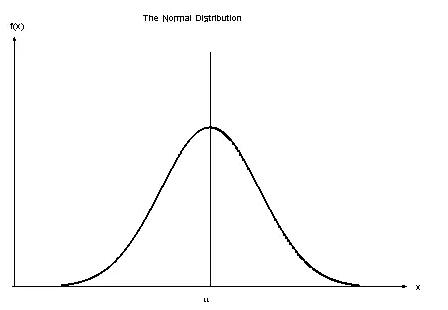
　　那這到底是一個怎樣的Distribution呢？

 

　　一般當我們說起Normal Distribution時，有兩個參數會顯得特別重要，它們分別是——平均值（mean）與方差（variance）。可以說，Normal Distribution就是由這兩個參數所決定的一個連續性（continuous）隨機變量（random variable）分布。

 

　　其中第一個參數mean決定了該分布的中心位置，而第二個參數variance（或者說standard deviation）則決定了中心位置附近數據的密度狀況。一般，variance值（standard deviation）越大，密度分布相應越分散，即，每個數據之間的間隔越大。
 

 

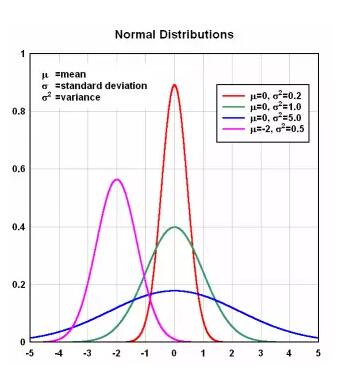
　　所以，在IB階段的我們，對Normal Distribution需要有哪些了解？

 

　　首先，當我們已知一個隨機變量屬于Normal Distribution時，我們需要能根據NormalDistribution的特有性質（如對稱性與連續性等），結合查表（Tableof Normal Distribution Function）來確定一個特定區間內對應的概率大小，在這個步驟中，我們同時還需要了解如何標準化（standardizing）一個NormalDistribution。其次，了解其他Distribution與Normal Distribution之間的潛在關系。

 

　　對于第一個大塊來說，最重要的能夠快速根據題意畫出合適的Normal Distribution圖。

 

　　一般題目類型分為，已知某個區間，想求出對應的probability，這種是最簡單的一種，首先運用標準化公式（公式1）。
 

 

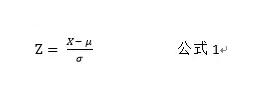
　　將題中給出的NormalDistribution轉化成Standard NormalDistribution，然后將平均值0放中間，畫出這個鐘型curve，最后按照轉化后得出的Z-score標注出題目中所問的區域，然后查表就可以得出結果啦。

 

　　除此之外，同學們很有可能會遇到反過來的這種題型，這種題目對將probability視為已知量，想反過來求取對應的區間，對于這種，其實大致的思路還是和前一種類似，只不過在畫圖的時候，需要根據probability的大小等已知量大約鎖定數據在mean值得左邊還是右邊，就可以輕松根據圖表得出答案啦。

 

　　對于第二個大塊，這可是NormalDistribution很關鍵的地方，其中涉及到各個Distribution與Normal Distribution的關系，及關系被滿足的條件等，小伙伴們一定記得好好復習哦~

 

　　好了，關于IB數學考點中NormalDistribution的內容就為大家介紹到這里了，大家是不是對于這部分有了更進一步認識了呢？更多IB數學考點解析，可以聯系A加未來IBDP一對一面授輔導班老師，在專業老師一對一指導下攻克數學學習難點，為更高的IB成績沖刺吧！